Interdisciplinary Research Group II

This team unites expertise across materials chemistry, physics, and biology to develop a comprehensive fundamental understanding of how elastic instabilities, such as wrinkling, creasing, and crumpling, can be harnessed to control polymer surface morphology and properties. IRG II researchers strive to deepen the fundamental understanding of molecular configuration and processing on wrinkle morphologies, the dynamic response of creasing, and the transfer of knowledge derived from polymer surface instabilities to complex material networks such as particle-based films.

Surface Wrinkles

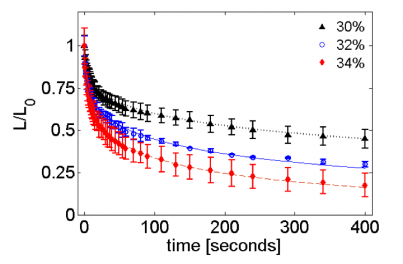A thin elastic layer placed under critical compressive stress accommodates applied strain by local bending, manifest as surface wrinkling rather than continued in-plane strain. Wrinkles are largely sinusoidal, their wavelengths defined by the thickness of the elastic layer and the mechanical properties of both the layer and supporting foundation. As noted by Cerda (Santiago) and coworkers, compression wrinkles arise from a one dimensional stress field, while tension wrinkles arise from a two-dimensional field. In both categories, wrinkles align normal to the compressive stress and represent the principle stress line. Wrinkles probe the stress field in delicate structures without changing the material or causing the material failure.  Menon and Russell exploit these attributes to address fundamental questions in surface science and polymer physics through experiments designed to clarify the simplest situation of planar tensional wrinkles. The spatial extent of wrinkle patterns at the center of an elastic annulus floating in a Langmuir trough was quantified. In this axisymmetric geometry, the tension at the inner boundary is kept constant, while the tension at the outer boundary is controlled by compression of an insoluble surfactant. The annuli consisted of polystyrene (PS) films of 62-180 nm thickness, floating freely on water. When the differential tension was increased beyond a threshold value, radial wrinkles formed in the interior of the annulus, and extended outwards. Measuring wrinkle length as a function of surface tension scales linearly, rather than as the square root of the differential tension, as previously believed. Investigating the viscoelastic relaxation of wrinkle pattern, Russell and Menon found that wrinkle patterns form upon placing a drop of water at the center of a floating polymer disc. The length and wavelength of the wrinkle decay, as shown in Fig 1, provide a measure of stress and strain and open the potential of making rheological measurements with a trivially simple apparatus on thin films.

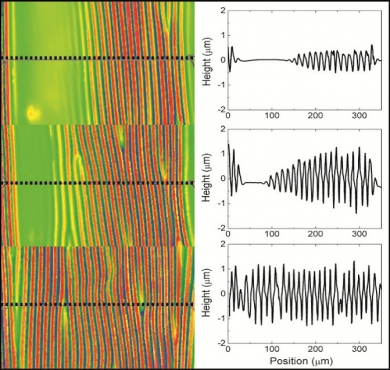In a complementary approach, Crosby worked to understand wrinkles in thin films supported by elastic substrates rather than fluids, focusing on quantifying the amplitude growth of wrinkled structures that are inhomogeneously distributed across a surface. While homogeneous strain will result in homogeneous wrinkling, a systematic understanding of pre-existing strain inhomogeneity, which is commonly found in practical materials, has remained elusive. As depicted in Fig 2, Crosby used a novel fabrication method to understand this effect, with the surprising finding that a surface with inhomogeneously distributed wrinkles develops wrinkles of homogeneous dimensions at small applied strains (~6%).

Surface Creasing

In contrast to surface wrinkling, a different and less-appreciated instability occurs when a soft elastic solid is placed under large compressive strains. This instability is termed 'creasing' since it results in the formation of sharp folds in the free surface of the material, distinct from the sinusoidal features formed by wrinkling. Hayward's collaboration with Suo (Harvard) characterized the role of surface energies in a creasing feature. Due to the inherently singular shape of creases, the surface energy penalty scales linearly with crease amplitude, compared to a quadratic scaling for elastic energy. In close analogy to classical nucleation in crystallization or phase separation, this yields an energetic barrier that causes creases to form by nucleation and growth rather than a simple bifurcation.

To quantitatively characterize this phenomenon, propagation of creases across films of gradient thickness (Fig. 3) was studied as a function of 1) surface energy between the elastomer and the medium; and 2) compressive strain. The resistance to crease propagation agreed closely with zero free parameter predictions from a scaling analysis and finite element modeling. Hayward and McCarthy contributed studies on using visible light as a switching stimulus to form creases on hydrogel surfaces. By incorporating light-absorbing iron oxide nanoparticles within a temperature-responsive poly(N-isopropyl acrylamide), highly reversible switching of crease patterns was achieved, with both global actuation and independent switching of single features.

Growth Kinetics for Morphology Control

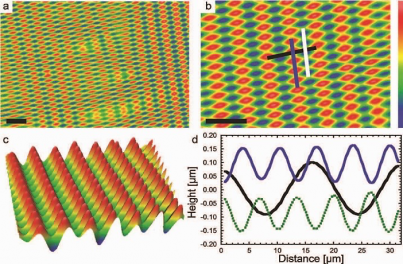IRG researchers deepened their quantitative understanding of top-constrained morphology as a function of crucial governing parameters: 1) the overstress, or ratio of applied stress to the critical buckling stress; and 2) the ratio of in-plane principal stresses. For equibiaxial stress states, wrinkle morphology transitions from dimple arrays to ridge patterns as the overstress increases from 1.0 to 1.5. With Suo and Hutchinson at Harvard, this narrow transition was modeled using both analytical and numerical methods. Crosby further investigated the control of new morphologies on biaxially wrinkled surfaces through a two-step application of sequentially applied uniaxial strains. Importantly, this formation process was studied as a function of the extent of crosslinking of the elastic substrate at each strain application. Wrinkle morphologies with two distinct, tunable orthogonal wavelengths on a single surface were observed (Fig. 4). Such biaxial wrinkle surfaces were achieved by 1) forming aligned wrinkles on a partially crosslinked soft substrate; 2) completing the crosslinking reaction of the substrate; and 3) applying a uniaxial strain orthogonal to the initial uniaxial strain direction. The modulus and thickness of the film remain constant throughout the process, but the modulus of the substrate was varied by more than an order of magnitude between the first and second strain applications.